2023.11.17
2023.11.16
2023.11.15
2023.11.14
2⃣ 三角形の内角と外角
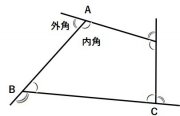
■外角と内角・・・右の図の四角形ABCDで、∠BAP
のように1つの辺ととなりの辺の延長とがつくる角を
その頂点における外角という。
また、∠BAD、∠ABCなどを内角という。
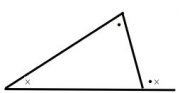
■三角形の内角、外角の性質
1⃣ 三角形の3つの内角の和は180°である。
2⃣ 三角形の1つの外角は、そのとなりにない2つ
の内角の和に等しい。
(例)
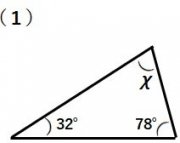
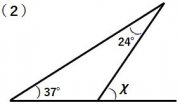
∠ χ =180°-(32°+78°) ∠ χ =24°+37°
=70° =61°
■鋭角・鈍角
① 鋭角・・・0°より大きく90°より小さい角を鋭角という。
② 鈍角・・・90°より大きく180°より小さい角を鈍角という。
三角形の分類
・鋭角三角形・・・3つの内角が鋭角
・直角三角形・・・1つの内角が直角
・鈍角三角形・・・1つの内角が鈍角

■外角と内角・・・右の図の四角形ABCDで、∠BAP
のように1つの辺ととなりの辺の延長とがつくる角を
その頂点における外角という。
また、∠BAD、∠ABCなどを内角という。

■三角形の内角、外角の性質
1⃣ 三角形の3つの内角の和は180°である。
2⃣ 三角形の1つの外角は、そのとなりにない2つ
の内角の和に等しい。
(例)


∠ χ =180°-(32°+78°) ∠ χ =24°+37°
=70° =61°
■鋭角・鈍角
① 鋭角・・・0°より大きく90°より小さい角を鋭角という。
② 鈍角・・・90°より大きく180°より小さい角を鈍角という。
三角形の分類
・鋭角三角形・・・3つの内角が鋭角
・直角三角形・・・1つの内角が直角
・鈍角三角形・・・1つの内角が鈍角
2023.11.13
1⃣ 対頂角、同位角、錯角
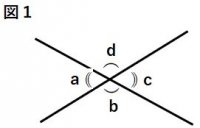
■対頂角・・・2つの直線が交わってできる4つの
角のうち向かい合っている角を対頂角という。
対頂角は等しい。
(例)右の図1で∠ aと∠c、∠bが対頂角であり
∠ a = ∠c,∠b=∠dである。
■同位角・・・右の図2のように、2つの直線 ℓ、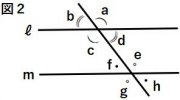
mに1つの直線が交わってできる角のうち、∠ aと
∠cのような位置にある角を同位角という。
(例)∠dと∠f、∠cと∠g、∠dと∠hもそれぞ
れ同位角である。
■錯覚・・・右の図2で∠cと∠ eのような位置にある角を錯角という。
(例)∠dと∠fも錯角である。
■平行線の性質
2つの直線に1つの直線が交わるとき、次のことが成り立つ。
1⃣ 2つの直線が平行ならば、同位角が等しい。
2⃣ 2つの直線が平行ならば、錯角は等しい。
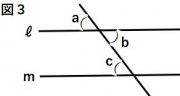
(例)右の図3でℓ∥mのとき
同位角は等しいから、∠ a=∠c
錯角は等しいから、 ∠b=∠c
■平行になる条件
2つの直線に1つの直線が交わるとき、次のことが成り立つ。
1⃣ 同位角が等しいならば、この2つの直線は平行である。
2⃣ 錯角が等しいならば、この2つの直線は平行である。
(例)右の図3で
∠ a =∠cならば、ℓ ∥ mである。
∠b=∠cならば、ℓ ∥ mである。

■対頂角・・・2つの直線が交わってできる4つの
角のうち向かい合っている角を対頂角という。
対頂角は等しい。
(例)右の図1で∠ aと∠c、∠bが対頂角であり
∠ a = ∠c,∠b=∠dである。
■同位角・・・右の図2のように、2つの直線 ℓ、

mに1つの直線が交わってできる角のうち、∠ aと
∠cのような位置にある角を同位角という。
(例)∠dと∠f、∠cと∠g、∠dと∠hもそれぞ
れ同位角である。
■錯覚・・・右の図2で∠cと∠ eのような位置にある角を錯角という。
(例)∠dと∠fも錯角である。
■平行線の性質
2つの直線に1つの直線が交わるとき、次のことが成り立つ。
1⃣ 2つの直線が平行ならば、同位角が等しい。
2⃣ 2つの直線が平行ならば、錯角は等しい。

(例)右の図3でℓ∥mのとき
同位角は等しいから、∠ a=∠c
錯角は等しいから、 ∠b=∠c
■平行になる条件
2つの直線に1つの直線が交わるとき、次のことが成り立つ。
1⃣ 同位角が等しいならば、この2つの直線は平行である。
2⃣ 錯角が等しいならば、この2つの直線は平行である。
(例)右の図3で
∠ a =∠cならば、ℓ ∥ mである。
∠b=∠cならば、ℓ ∥ mである。