■ 一般動詞の過去形(規則動詞)
【34】Tell me about your weekend . 私にあなたの週末について教えてください。
I stayed home and watched TV . 私は家にいてテレビを見ました。
一般動詞の過去形(規則動詞) : 「~しました」と過去のことを表すときは、ふつう一般動詞の語尾に
ー(e)dをつける。このような動詞を規則動詞といい、主語が何であっても同じ形になる。
〈現在の文〉 I play soccer every day . (私は毎日サッカーをします。)
He plays soccer every day . (彼は毎日サッカーをします。)
〈過去の文〉 I played soccer last Sunday . (私はこの前の日曜日、サッカーをしました。)
He played soccer last Sunday . (彼はこの前の日曜日、サッカーをしました。)
⇖主語が何であっても過去形は同じ形
※一般動詞の過去形の作り方
・ふつう ⇒ そのままーedをつける [例]work → worked clean → cleaned
・e で終わる語 ⇒ ーdだけをつける [例]use → used like → liked
・〈子音字+y〉で終わる語 ⇒ yをiにかえてーedをつける [例]study → studied
・〈短母音+子音字〉で終わる語 ⇒ 子音字を重ねてーedをつける [例]stop「止まる」 → stopped
■ 絵や写真の説明の仕方
① 絵や写真の中にだれがいるか[何があるか]説明する。
There is a ~ in the picture . (絵[写真]の中に(1人[1つ]の)~がいます[あります]。)
関連 2人[2つ]以上の人物やものについて言うときは、There are ~ .の文にする。
② 絵の中の人物やものについての状況や特徴を説明する。
The man is sitting on the chair . (その男の人はいすにすわっています。)
The dogs are running in the park . (その犬たちは公園で走っています。)
The girl is wearing a blue jacket . (その少女は青いジャケットを着ています。)
Some children are singing together . (何人かの子供たちがいっしょに歌っています。)
【要点整理】
「(今)~しています、~しているところです」と、動作が進行していることを表す文を現在進行形の文
という。
① 現在進行形は〈be動詞(am , are , is)+動詞の-ing形〉で表す。be動詞は主語によって使い分ける。
② 否定文・・・〈主語+am[are , is]+ not +動詞の-ing形~.〉で表す。
③ 疑問文・・・〈Are[Is , Am]+主語+動詞の-ing形~?〉で表す。答えるときもbe動詞を使う。
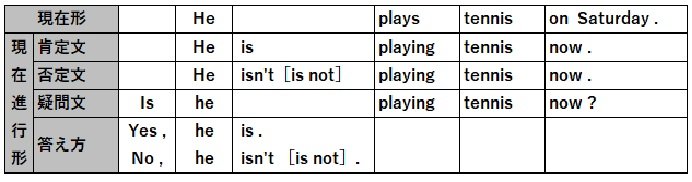
■ 現在進行形 の疑問文 / What ...~ing ? の文
【32】Are you really studying , Ben ? あなたはほうとうに勉強をしているところですか、ベン。
現在進行形の疑問文 : 「(今)~していますか」「~しているところですか」という疑問文はbe動詞の
主語の前に置いて〈Are[Is , Am]+主語+動詞の-ing形~?〉で表す。答える
ときもbe動詞を使う。
〈肯定文〉 you are studying English . (⤵) (あなたは英語を勉強しています。)
〈疑問文〉 Are you studying English ? (⤴) (あなたは英語を勉強していますか。)
〈答え方〉 Yes , I am . / No , I'm not . (はい、しています。 / いいえ、していません。)
【33】What are you doing ? あなたは何をしているのですか。
I'm reading an important book . 私は大事な本を読んでいるところです。
What...~ing?の文 : 「(今)何をしていますか」という疑問文は〈What+are[is , am]+主語
+doing?〉で表す。「(今)何を~していますか」とたずねるときは〈What+
are[is , am]+主語+動詞の-ing形?〉で表す。
Are you studying English ? (⤴) (あなたは英語を勉強していますか。)
What are you doing ? (⤵) (あなたは何をしていますか。)
What are you studying ? (⤵) (あなたは何を勉強していますか。)
■ 現在進行形 / 現在進行形の否定文
【30】I'm studying now . 私は今、勉強をしているところです。
現在進行形 : 「(今)~しています」「~しているところです」と、動作が進行していることを表す文を
現在進行形の文という。現在進行形は〈be動詞(am , are , is)+動詞の-ing形〉で表す。
be動詞は主語によって使い分ける。
〈現在形の文〉 I play soccer every day . (私は毎日サッカーをします。)
〈現在進行形の文〉 I am playing soccer now . (私は今、サッカーをしています。)
※-ing形の作り方
・ふつう ⇒ 語尾に-ingをつける [例]play → playing study → studying listen → listening
・eで終わる語 ⇒ eをとって-ingをつける [例]come → coming take → taking
・〈短母音+子音字〉で終わる語 ⇒ 子音字を重ねて-ingをつける [例]run → running
swim → swimming
【31】I'm not doing anything now . 私は今は何もしていません。
現在進行形の否定文 : 「(今)~してません」「~しているところではありません」という否定文は
be動詞のうしろにnotを置いて〈主語+am[are,is]+not+動詞-ing形~.〉で
表す。
I am not playing soccer now . (私は今、サッカーをしていません。)







