浜松南教室のメッセージ
静岡県公立高校入試 数学 大問6 2025年度
2025.02.01

①問題文を読んだ後に
関数の問題を解くために、問題文の情報を整理するために、座標やグラフの式が読み取ることができるようにします。
上のように問題文の情報もグラフにも書き込みましょう。
②(1)yの変域を求める
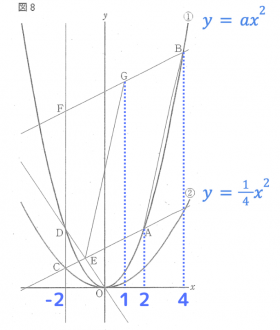
②の2次関数のグラフは、上に開いた放物線です。
問題の座標の範囲はx=−2とx=3です。
そのため、x=2とx=3を比較するとx=3が最大値になります。

したがって、yの変域は、 となります。
③(2)ア 直線傾きを求める
直線OAは、原点を通る比例のグラフです。
点Aのx座標は2であり、①のグラフが通るので、

となり、点Aの座標は、( 2 , 4a )と表すことができます。
比例のグラフの傾きは、xの値とyの値の商になるので、
となります。
④(2)イ四角形GEABが平行四辺形になるときのaの値
四角形GEABが平行四辺形になるので、それをもとにaの値を考えていきます。
平行四辺形は対辺が平行であり、直線ACと直線BGも平行になるため、グラフの傾きが等しくなります。
直線ACと直線BGの傾きを計算して、aの値を求めます。
直線ACと直線BGの傾きを計算するために必要な点Aと点B、点C、点Gの座標を求めます。
点Aの座標 点Aの座標は、(2)アの計算過程より、( 2 , 4a )。
点Bの座標 点Bの座標は、x座標が 4 であり、①のグラフが通るので、

となり、点Aの座標は、( 4 , 16a )。
点Cの座標 点Cの座標は、x座標が-2であり、②のグラフが通るので、
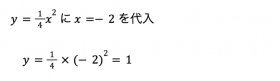
となり、点Cの座標は、( -2 , 1 )。
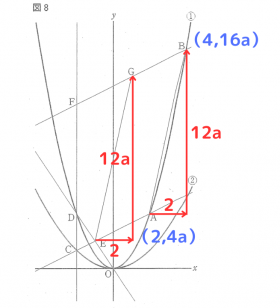
点Gの座標 点Gの座標を求めるために、点Eの座標から考えます。
上図のように、点Bは点Aから、x軸方向に2、y軸方向に12aだけ移動させた点であることが読み取れます。
四角形GEABは平行四辺形なので、点Eと点Gでも同様に移動させることで座標を考えることができます。
点Gのx座標は1なので、点Eのx座標は-1であることが分かります。
点Eのx座標が1、点DのX座標が2なので、点Eは線分ODの中点ということが読み取れます。
よって、点Eのy座標は2aになり、点Eの座標は( -1 , 2a )となります。
点Eの座標からx軸方向に2、y軸方向に12aだけ移動させた点が点Gなので、点Gの座標は( 1 , 14a )になります。
次に、直線ACと直線BGの傾きを使ってaの値を計算します。 直線の傾きは、変化の割合と同じ値なので、
で計算することができます。
直線ACの傾きと直線BGの傾きは等しいので、