浜松南教室のメッセージ
静岡県公立高校入試 数学 大問7 2025年度
2025.02.01
△AFEと△BGPにおいて
FE//BCより同位角は等しいので
∠AEF = ∠ACB ・・・①
弧ABの円周角より
∠BPG = ∠ACB ・・・②
①,②より
∠AEF = ∠BPG ・・・③
仮定より
CA = CD ・・・④
BA = BG ・・・⑤
④より△CADは二等辺三角形であり底角は等しいので
∠CAP = CDA ・・・⑥
⑤より△BAGは二等辺三角形であり底角は等しいので
∠BAG = ∠BGA ・・・⑦
弧ADの円周角より
∠ABG = ∠ABD ・・・⑧
⑥,⑦,⑧より△CADと△BAGは頂角が等しい二等辺三角形なので
∠BAG = ∠CAD ・・・⑨
弧PDの円周角より
∠PBG = ∠PAD ・・・⑩
また
∠EAF = ∠BAG - ∠CAP ・・・⑪
∠PAD = ∠CAD - ∠CAP ・・・⑫
⑨,⑪,⑫より
∠PAD = ∠EAF ・・・⑬
⑩,⑬より
∠EAF = ∠PBG ・・・⑭
③,⑭より、2組の角がそれぞれ等しいので
△AFE ≡ △BGP
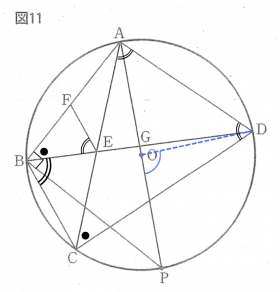
上図のように、補助線として線分ODを引く
FE//BCより
錯角は等しいので
∠FEB = ∠DBC = 68°
弧CDの円周角より
∠DBC = ∠CAD = 68°
CA = CDより
CADは二等辺三角形であり、その底角は等しいので
∠CAD = ∠CDA = 68°
したがって
∠ACD(図中の⚫︎)は∠ACD = 180° - 68° × 2 = 44°
弧ADの円周角より
∠ACD = ∠ABD = 44°
線分APは円Oの半径なので
∠ABP = 90°
よって
∠DBP は∠DBP = ∠ABP - ∠ABD = 90° - 44° = 46°
中心角∠PODは、円周角∠DBPの2倍の大きさになるので
∠POD = 2 × ∠DBP = 2 × 46° = 92°
したがって、おうぎ形OPDの弧DPの長さは、






