城南コベッツ浜松南教室

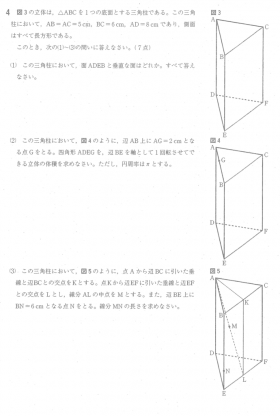
(1) 空間図形の三角柱の1つの側面と垂直な関係にある面を答える問題
立体の図形をイメージしていくと、
図3より、面ADEBと垂直な面は、 面ABC , 面DEF の2つ

(2) 立体の体積
四角形ADEGを1回転させてできる立体の体積を考え、まず下図のように四角形ADEGの各辺の長さを整理。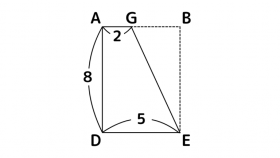

次に、辺BEを軸として1回転させてできる立体の見取り図と各辺の長さは下図の通り。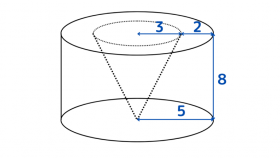


上図より、四角形ADEGを辺BEを軸として1回転させてできる立体の体積は、 円柱の体積から円錐の体積を引いて求めることができる。
体積を計算。




(3) 立体の中の線分の長さ 線分MNの長さを計算するために、下図のような補助線を引く。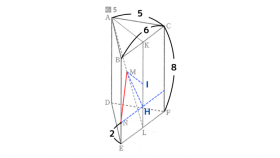

必要な補助線は、下記の通りです。
点Nから線分EFと並行な直線を引き、線分KLとの交点をHとして、線分MHを引く。
線分KLの中点をIとして、線分MIを引く。

① 線分MIの長さ 線分MIの長さを求めるために、線分AKの長さを計算します。 AB = 5cm , BK = 3cmより、三平方の定理から、


また、AM = LM , KI = LI なので、中点連結定理より、


② 線分MHの長さ 次に、線分MHの長さを△IMHの辺の長さを使って計算。
IL = 4cm , HL = 2cmより、IH = 4 -2 = 2cmに。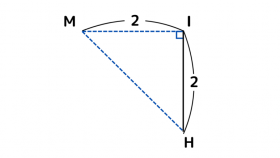

上図から、△IMHは∠MIH = 90° の直角二等辺三角形である。
直角二等辺三角形の辺の比は、


なので、線分MHの長さは、


③ 線分MNの長さ △MNHの辺の長さを使って、線分MNの長さを計算。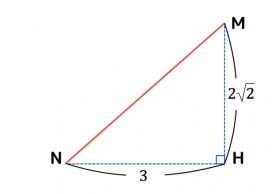