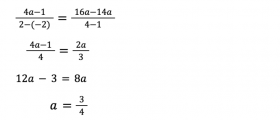2025.03.05
2025.02.17
1次検定合格おめでとうございます！
ギリギリでしたが、よく頑張りましたね！
中学校時代、最初はそれほど得意ではなかった英語ですが、少しずつ力を伸ばしていきました。
高校に入っても、普段から一生懸命に頑張って勉強を続けてきました。
日頃の勉強が頑張りが見事発揮されましたね。
英検２級は単語も文法も簡単ではないため、難易度は高いです。
塾長も英検準1級を取得しているので大変さはよくわかります。
チャレンジで受検しましたが、本当によく頑張りました。
2次試験も一緒に頑張りましょう！！
生徒さんの英検２級1次試験の合格証（２０２５,２）
浜松市中央区三島町の個別指導塾城南コベッツ浜松南教室
2025.02.01
本文全訳
健と私はクラスメートです。
彼は私の家の近くに住んでおり、私たちは10年来の友達です。彼はテニスが得意です。
ある日、私たちは体育の授業でテニスをしました。
それは私が初めてテニスを試みる日でした。
最初に、先生と健が私たちにボールの打ち方を見せてくれました。
それから、私たちはラケットを持って練習を始めました。
私は健と一緒に練習しました。
彼はゆっくりと私にボールを打ってくれましたが、私はそのボールを返すことができませんでした。
何度も挑戦してベストを尽くしましたが、彼にボールを返すのは私には難しかったです。
体育の授業が終わったとき、私は健に「ごめんね。私がテニスをうまくできなかったから、今日は十分にテニスの練習ができなかったよね」と言いました。
彼は「気にしないで。誰でも最初は初心者だから。その代わり、新しいことに挑戦するのを楽しんで！」と言いました。
彼の言葉は私に再びテニスに挑戦する力を与えてくれました。
次の体育の授業では、私は前向きになることを決めました。
健や他のクラスメートに、なぜうまくボールを打てないのかを尋ね、一緒にいろいろな練習を試しました。
ついに、授業の終わりには、私はボールを返すことができました。
ボールは健に届き、彼はそれを私に打ち返し、私は再びそれを打ちました。
それは私を興奮させました。
翌朝、教室に着くと、健がとてもゆっくりとキーボードを弾いていました。
「わあ、キーボードを練習しているの？」と私は言いました。
彼は「うん。駅にあるピアノを知ってる？先月、そこでとても上手に弾いている男の子を見かけて、キーボードを練習しようと決めたんだ」と言いました。
私は「キーボードを弾くのを習ったことがないから、難しいでしょ？」と言いました。
健は「うん。あの男の子みたいに指を速く動かせないけど、新しいことに挑戦するのを楽しんでいるよ」と言いました。
私は体育の授業での健の言葉を思い出しました。
1か月後の体育の授業の後、私は健と話しました。
「体育の授業でテニスをするのはとても楽しかったけど、それが終わってしまった。もっとテニスをしたいな」と私は言いました。
彼は「そう思うなら、町のテニスチームに参加しようよ。おじいちゃんが毎週日曜日にそのチームでテニスをしているよ。メンバーはみんな君より年上だけど、みんな親切だよ」と言いました。
「面白そう。チームに参加したい」と私は言いました。
次の日曜日の朝、私はテニスチームの練習に参加するために公園に行きました。
チームには中学生はいませんでした。
しかし、テニスチームのメンバーは親切で前向きだったので、彼らと一緒にテニスを楽しむことができました。
彼らがうまくボールを打てないときでも、悲しそうには見えませんでした。
健のおじいちゃんは私に「次はきっとボールを返せると信じているよ。自分を信じているんだ」と言いました。
練習の後、私は「新しいことを楽しむことと同じくらい、自分が何でもできると信じることも重要なんだ。新しいことを始めてうまくいかないときは、そのことを思い出そう」と考えました。
(1)解答 a：held b：older
動詞と形容詞の変形の問題です。
該当する文章の文法を見て、適切な形に直しましょう。
aは、文頭に「Then」があり、過去形か未来形の予想ができます。
bは、該当の英単語の後ろに「than」がきているので、比較級ということがわかります。
教科書に掲載されている不規則動詞などは一通り練習しておきましょう。
(2) 解答例 ①：For ten years. ②：Because they were friendly and positive.
英問英答=英語で書かれた質問に英語で答える英作文問題です。
本文中の該当場所を探して、正確に回答しましょう。
(3) 解答 ウ
空欄補充 (3)は、本文中の空欄に適切な文章を補う選択肢の問題です。
前後の文脈を読んで判断しましょう。
[ A ]は、本文7行目の該当する文章の前半を確認すると、「今日は十分にテニスの練習ができなかったよね」と謝った内容が書かれていて、「because」と続くので、その理由が該当します。
[ B ]は、本文9行目の段落から読み進めると、「健や他のクラスメートに、なぜうまくボールを打てないのかを尋ね、一緒にいろいろな練習を試しました。」と書いてあり、そして「Finally」と続いているため、ついにうまくボールを打つことができた、とう文章が続くことが読み取れます。
(4) 解答例 ピアノがとても上手な男の子を駅で見たできごと。
和問和答 =日本語で書かれている質問に対して、日本語で回答する問題です。
本文16行目を参考に回答しましょう。
(5) 解答 エ
空欄補充 =本文中の空欄に適切な文章を補う選択肢の問題です。
本文の前後の文脈で判断しましょう。
空欄の前の文章では、「体育の授業でテニスをするのはとても楽しかったけど、それが終わってしまった。」といった内容の文章が書かれています。
そして、空欄の後の文章では、健が町のテニスチームへの参加をお勧めしています。
これらのことから、空欄は、志保がテニスを続けたい、もっとやりたいとい内容った内容であったことが読み取れます。
(6) 解答例 自分は、何でもできると信じることは、新しいことを楽しむことと同じくらい大切であること。
和問和答=日本語で書かれている質問に対して、日本語で回答する問題です。
本文最後の段落に書いてある志保の主張部分を参考に日本語でまとめましょう。
(7)解答 ア
内容把握=本文の内容と合うものを選ぶ選択問題です。
本文の内容と明らかに違う点が含まれる選択肢を削除して、消去法で考えましょう。
選択肢イは、志保が最初にテニスがうまくできなかった時、様々な練習をしようと先生が言ったのではなく、志保が健や他のクラスメイトに聞いたと書かれています。
選択肢ウは、本文中に健がキーボードが上手になったという文章はないため間違いです。
選択肢エは、本文とは全く関係のない文章です。
2025.02.01
(1) 作図
作図の問題では、 問題文に書かれている2つの条件にあった点を作図する問題 が頻出です。
問題文の条件に沿った直線を2本を作図して、 その交点が答えとなることが多い。
この問題の作図の条件は、下記の2つです。
条件①：円の中心Oは、2辺BC, ACから等しい距離にあること。
条件②：円Oは、2点A, Cを通ること。
この条件に従って、作図を進めていきます。
条件①：角の二等分線の作図
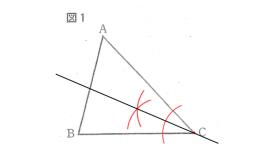
2辺BC, ACから等しい距離にある点は、∠Cの二等分線上の点となります。
上図の手順で、∠Cの二等分線を作図します。
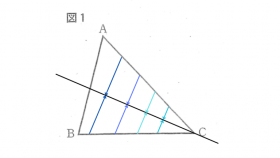
上図のように、∠Cの二等分線上の点はどこを取っても2辺BC, ACからの距離は等しいことが分かります。
条件②：垂直二等分線の作図
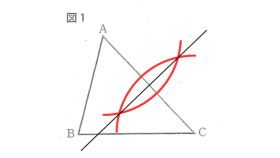
円Oは、2点A, Cを通るので、円の中心Oは、線分ACの垂直二等分線上にあることが分かります。
上図の手順で、線分ACの垂直二等分線を作図します。
(1) 作図の解答
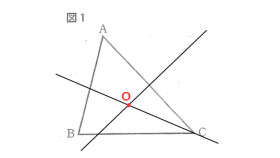
条件①と条件②で作図した直線の交点が点Oとります。
コンパスで描いた作図の跡は、消さずにのことしておきましょう。
(2) 比例・反比例の式
(2)は、2つの数値の関係性を見付けて、式で表す問題です。
問題文から、水槽の容量である90 Lは変化しない定数であることが読み取れます。
また、毎分水を入れる量のx Lを増やすと、満水になるまでにかかる時間が減少する関係であることが分かります。
xとyの関係をまとめたものが、下記の表になります。
xの値が2倍、3倍、4倍...になると、yの値が1/2倍、1/3倍、1/4倍になっていることが読み取れます。
したがって、このxとyは、反比例の関係であることが分かります。
反比例の一般式は、
また、上記の表から、xとyの積が必ず90に一定となることから、比例定数は90です。 よって、yをxの式で表すと、
(3) 確率
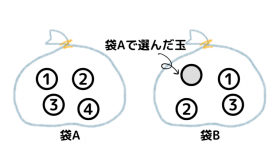
上記の図ように、袋Aと袋Bの両方に4つの玉が入っているもととして考えます。
下記の図は、袋Aから1個の玉を取り出して、その玉を袋B入れてから1個の玉を取り出すときの取り出し方を表した樹形図です。
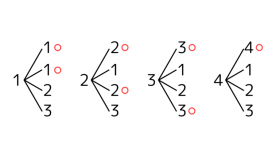
上記の樹形図より、 玉を取り出す組み合わせの総数は16通り、 袋Aと袋Bの両方から同じ数字を取り出す組み合わせ（赤い⚪︎）の総数は7通り です。
したがって、解答は、
2025.02.01
①問題文を読んだ後に
関数の問題を解くために、問題文の情報を整理するために、座標やグラフの式が読み取ることができるようにします。
上のように問題文の情報もグラフにも書き込みましょう。
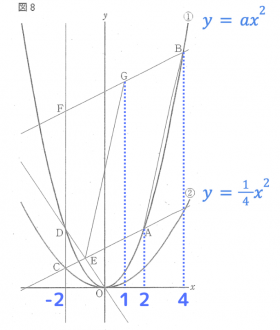
②（１）ｙの変域を求める
②の２次関数のグラフは、上に開いた放物線です。
問題の座標の範囲はx=−2とx=3です。
そのため、ｘ＝２とｘ＝３を比較するとｘ＝３が最大値になります。
したがって、yの変域は、 となります。
③（２）ア 直線傾きを求める
直線OAは、原点を通る比例のグラフです。
点Aのx座標は2であり、①のグラフが通るので、
となり、点Aの座標は、（ 2 , 4a ）と表すことができます。
比例のグラフの傾きは、xの値とyの値の商になるので、
となります。
④（２）イ四角形GEABが平行四辺形になるときのａの値
四角形GEABが平行四辺形になるので、それをもとにaの値を考えていきます。
平行四辺形は対辺が平行であり、直線ACと直線BGも平行になるため、グラフの傾きが等しくなります。
直線ACと直線BGの傾きを計算して、aの値を求めます。
直線ACと直線BGの傾きを計算するために必要な点Aと点B、点C、点Gの座標を求めます。
点Aの座標 点Aの座標は、(2)アの計算過程より、（ 2 , 4a ）。
点Bの座標 点Bの座標は、x座標が 4 であり、①のグラフが通るので、
となり、点Aの座標は、（ 4 , 16a ）。
点Cの座標 点Cの座標は、x座標が-2であり、②のグラフが通るので、
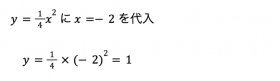
となり、点Cの座標は、（ -2 , 1 ）。
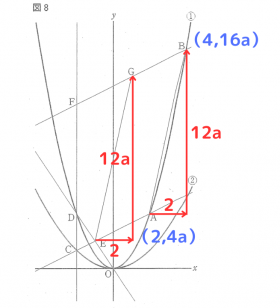
点Gの座標 点Gの座標を求めるために、点Eの座標から考えます。
上図のように、点Bは点Aから、x軸方向に2、y軸方向に12aだけ移動させた点であることが読み取れます。
四角形GEABは平行四辺形なので、点Eと点Gでも同様に移動させることで座標を考えることができます。
点Gのx座標は1なので、点Eのx座標は-1であることが分かります。
点Eのx座標が1、点DのX座標が2なので、点Eは線分ODの中点ということが読み取れます。
よって、点Eのy座標は2aになり、点Eの座標は（ -1 , 2a ）となります。
点Eの座標からx軸方向に2、y軸方向に12aだけ移動させた点が点Gなので、点Gの座標は（ 1 , 14a ）になります。
次に、直線ACと直線BGの傾きを使ってaの値を計算します。 直線の傾きは、変化の割合と同じ値なので、
で計算することができます。
直線ACの傾きと直線BGの傾きは等しいので、
